06. 图
图的关键词
- 完全图
- 无向图需要有 n(n-1)/2 条边。
- 有向图需要有 n(n-1)条弧。
- 邻接点
- 度(有向图还有出度和入度)
- 子图
- 路径
- 路径长度
- 简单路径:顶点不重复出现的路径。
- 回路:第一个顶点和最后一个顶点相同的路径。
- 简单回路:除第一顶点和最后以顶点外,其余顶点不重复出现的回路。
- 权:在图的每条边上加数字作权。
- 网:带权的图称为网。
-
连通:无向图中,如果从顶点 v 到顶点 v~有路径,则称 v 和 v~是连通的。
-
连通图:如果图中任意两个顶点都是连通的,则是连通图。
-
连通分量相关:
- 也叫无向图的极大连通子图
- 连通图只有一个连通分量,即其自身
- 非连通的无向图有多个连通分量
-
强连通图:有向图中每一对顶点都存在路径,则称 G 是强连通图。
-
强连通分量:
- 有向图的极大连通子图称作强连通分量。
- 强连通图的强连通分量是其自身
- 非强连通的有向图可能有多个强连通分量
-
生成树
- 一个连通图的极小连通子图
- 含有图中全部 n 个顶点,但只有能令图连通的 n-1 条边
图的存储
邻接矩阵
创建顶点集和创建关系集
//图的邻接矩阵存储
#define NMAX 100
typedef int datatype;
typedef struct{
datatype vexes[NMAX+1];
int edge[NMAX+1][NMAX+1];
int n,e
}graph;
graph *ga;
算法思路:
step1:创建 ga 的存储空间
step2:输入边数 ga->e
step3:输入顶点数 ga->n
step4:初始化顶点集 ga->vexes
foreach k in (1~ga->n)
输入顶点的数据 data
ga->vexes[k]=data
step5:初始化邻接矩阵 ga->edges 为全 0
step6:创建边集
foreach k in (1~ga->e)
输入边的顶点偶对:(i,j)
ga->edges[i][j]=1
ga->edges[j][i]=1
step7:return ga
邻接表
顶点表
边表:边表结点保存着与某顶点关联的另一顶点和指向下一表结点的指针
邻接表结构定义:
#define NMAX 100 //顶点的最大数
typedef struct node{ //边表结点
int vertex;
struct node* next;
}edgenode;
typedef struct{ //顶点表结点
vextype data;
edgenode* head; //边表头指针
}vexnode;
typedef struct{ //图的定义
vexnode vexes[NMAX+1]; //顶点表
int n, e; //顶点数、边数
}graph;
graph *ga;
算法思路:
#初始化顶点表 ga->vexes
for k in (1~ga->n):
# 输入数据 data
ga->vexes[k].data = data
ga->vexes[k].head = NULL
#创建边表集
for k in (1~ga->e):
# 输入边的顶点对(i,j)
# 将顶点 j 添加到顶点 i 的边表中
# 生成边表结点 p
# 结点数据域赋值:p->vertex=j
# 在边表中加入结点 p
# p->next=ga->vertex[i].head
# ga->vertex[i].head=p
# 将顶点 i 添加到顶点 j 的边表中
十字链表
//边表结点
typedef struct arctype{
int tailvex, headvex;
struct arctype *hlink,*tlink;
}arclink;
//顶点表结点
typedef struct vnode{
vertex data;
arclink *firstin, *firstout;
}ortholistNode
ortholistNode graph[NMAX];
边集数组
typedef struct{
int fromvex;//边的起点
int endvex;//边的终点
int weight;//边的权值
}EDGE;
EDGE edgeet[MaxEDGEnUM];
图的遍历
要求:无重复、无遗漏。
关键点:
- 图中可能存在回路。
- 顶点可能与其它顶点相通,访问完某顶点后,可能沿着某些边回到曾经访问过的顶点。
- 为避免重复访问,可设辅助数组 visited[]
- 将其初始化为 0.
- 遍历时,如果某顶点 i 被访问,将 visited[i]置为 1。
- 以此防止顶点 i 被多次访问。
深度优先(递归解法):
//邻接矩阵:
for k in (1~n)
visied[i] = 0;
DFS(ga, vi){
visit(vi); //访问结点 vi
visited[vi]=1;
for k in (1~n){
if(ga->edges[vi][k] == 1 && !visited[k])
DFS(ga, k);
}
}
//邻接表:
for k in (1~n)
visied[i] = 0;
DFS(ga, vi){
visit(vi);
visited[vi] = 1;
p=(ga->vexes[vi]).head;
while(p){
if(!visited[p->vertex])
DFS(ga, p->vertex);
p=p->next;
}
}
深度优先(栈):
step1:设初始状态:图中所有顶点都没被访问过
foreach i in (1~n)
visited[i] = 0;
step2:初始化栈 stack
step3:c=r,push(stack,c) //r 为出发顶点的编号
step4:访问顶点 vc,令 visited[c]=1
step5:找到并访问与顶点 vc 邻接,但未被访问过的顶点 v_j
for(j:1~n)
if(ga[c][j] == 1 and visited[j] == 0)
c = j, push(stack, j)转 step4
step6:当 vc 所有的邻接点均被访问过,则退回到最近被访问的前一顶点。
if(!emptystack(stack))
c=pop(stack),转 step5
else return;
广度优先:类似于树的层次遍历,使用队列辅助存储。
图的连通性:如果遍历完成时 DFS 或 BFS 仅调用一次,则图是连通图;若被调用多次,则图是非连通图,分别访问多个连通分量。
图的拓扑排序
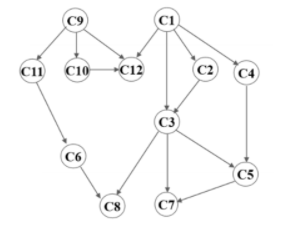
AOV:
- 顶点表示活动,弧表示活动间的先后关系。
- AOV 网中不能有回路,回路意味着某项活动以自己为先决条件。
- 死锁。
拓扑排序:
- 把 AOV 网中各顶点按其活动的先后关系,排列成一个线性序列的过程。
- 拓扑序列
- AOV 网用邻接表存储
- 在邻接表的表头结点增加存放顶点入度的域。
- 栈或队列存放入度为零的顶点。
拓扑排序:对有 n 个顶点的有向图 ga,以邻接表方式存储,找出一条拓扑序列。
step1:初始化栈 stack,令 count=0
step2:创建 ga 的邻接表,初始化每个顶点的入度为 0
step3:将当前可开始的活动入栈
foreach k in 1~n
if(ga->vexes[k].indegree==0)
push(stack, k)
step4:while(!empty(stack))
vi = pop(stack)
visit(vi),count++
将后续活动的入度减 1,并记录新的可开始的活动。
p=ga->vexes[vi].head
while(p)
ga->vexes[p->data].indegree--
if(ga->vexes[p->data].indegree==0)
push(stack,p->data)
p = p->next;
step3:如仍有活动未进行,return FALSE,否则 return TRUE
if(count<n)
return FALSE;
图的最小生成树
生成树
- 连通图 G 的极小连通子图,称为图的生成树
- 包含图中所有顶点
- 无回路
- n 个顶点,只有 n-1 条边。
- 任意去掉一条边,图将变为非连通图
- 添加一条边,图中将出现回路
- 含 n 个顶点 n-1 的图不一定是最小生成树
- 深度优先生成树
- 广度优先生成树
- 图的生成树不是唯一的
- 从不同的顶点出发,可得到不同的生成树。
图的最小生成树
- 连通网络 G=(V,E)的各边带权
- 因此其生成树各边带权
- 生成树的权
- 最小生成树(MST)
PRIM 算法
初始 U 中含任意一个顶点 u0,初始候选边集
- numv=1
- while(numv=1){
- 从 C 中选最短边并入边集 E,点集 U
- numv++
- 调整候选边集 C
Kruskal 算法
算法思想:权值由小到大开始来连接,连通的不要,直到生成生成树,即最小生成树。
