09. 算法概述#

最大公约数求解#

求两个不全为 0 的非负整数（m 和 n）的最大公约数（记作 gcd(m, n)）。

中学的计算方法#

• 找到 m 的所有质因数；
• 找到 n 的所有质因数；
• 找出所有的公因数；
• 将找到的公因数相乘，结果即为最大公约数；

60 = 2*2*3*5
24 = 2*2*2*3
gcd(60, 24) = 2*2*3 = 12

欧几里得算法#

• 如果 n = 0，返回 m 的值作为结果，过程结束；否则，进入第二步；
• m 除以 n，得到余数 r；
• 将 n 的值赋给 m，将 r 的值赋给 n，返回第一步；

gcd(60, 24) = gcd(24, 60 mod 24) = gcd(24, 12)
			= gcd(12, 24 mod 12) = gcd(12, 0) = 12

# 欧几里得算法伪代码
def Euclid(m, n):
    while n != 0:
        r = m mod n
        m = n
        n = r
    return m

连续整数检测法#

• 将 min(m, n)的值赋给 t；
• m 除以 t，如果余数为 0，进入第 3 步，否则进入第 4 步；
• n 除以 t，如果余数为 0，返回 t 的值，否则进入第 4 步；
• 将 t 的值减 1，返回第 2 步；

# TODO

算法的定义#

• 数学：

  算法通常是指按照一定规则解决某一类问题的明确和有限的步骤。

• 广义：

  • 算法是完成某项工作的方法和步骤：
    • 菜谱是做菜的算法；
    • 歌谱是一首歌曲的算法；

• 计算机科学

  算法是解决问题的一系列明确指令，也就是说，对于符合一定规范的输入，能够在有限时间内获得要求的输出。

算法的特点#

• 明确性
• 有限性
• 一般性
• 有序性
• 不唯一性

常见问题#

排序#

选择排序#

扫描整个列表，找到最小元素，和第 1 个元素交换；然后从第 2 个元素开始扫描列表，找到后面 n − 1 个元素的最小值，和第 2 个元素交换位置；如此重复。

'''
输入: 一个杂乱的数据 A[0...n − 1]
输出: 升序排列的数据 A[0...n − 1]
'''
function Selection_Sort(A[0...n − 1])
    for i = (0 , n − 2) do
        min = i //min 为最小元素索引
        for j = (i + 1 , n − 1) do
            if A[j] < A[min] then
                min = j
            end if
        end for
        swap A[i] and A[min]
    end for
end function

冒泡排序#

比较相邻元素，如果它们逆序就交换它们的位置，重复多次以后最大的元素就放置到最后的位置；如此放置次大的元素至倒数第 2 个位置；重复此过程。

'''
输入: 一个杂乱的数据 A[0...n − 1]
输出: 升序排列的数据 A[0...n − 1]
'''
function Bubble_Sort(A[0...n − 1])
    for i = (0 , n − 2) do
        for j = (0 , n − 2 − i) do
            if A[j + 1] < A[j] then
                swap A[j] and A[j + 1]
            end if
        end for
    end for
end function

查找#

顺序查找#

折半查找#

字符串处理#

蛮力匹配#

图#

拓扑排序#

地图四染色#

旅行商问题#

组合问题#

背包问题#

分配问题#

最近对问题#

几何问题#

凸包问题#

数值问题#

整数相乘#

算法效率分析#

输入规模：几乎所有的算法，运行时间都随着输入规模的增大而增大

渐进符号#

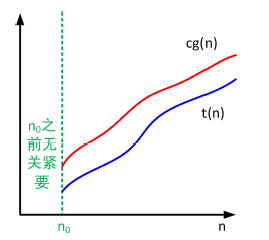
上界$O$的定义#

如果存在大于 0 的常数 $c$ 和非负整数 $n_0$ ，使得 $\forall n > n_0，t(n) \leqslant cg(n)$，我们称函 数 $t(n)$ 包含在 $O(g(n))$ 中，记作 $t(n)\in O(g(n))$。

下界$\Omega$的定义#

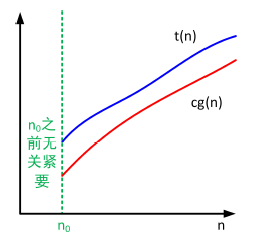
如果存在大于 0 的常数 c 和非负整数$n_0$，使得$\forall n > n_0$，$t(n) > cg(n)$，我们称函数 $t(n) $ 包含在 $\Omega(g(n))$ 中，记作 $t(n) \in \Omega(g(n))$。

$\theta$的定义#

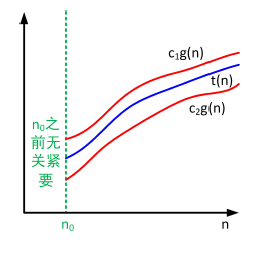
若存在大于 0 的常数$c1,c2$和非负整数$n_0,\forall n > n_0,c_1g(n) \leqslant t(n) \leqslant c_2g(n)$,我们称函数 t(n)包含在 $\theta(g(n))$ 中，记作 $t(n) \in \theta(g(n))$。

算法的三种效率#

• 最差效率$C_{worst}(n)$：输入规模为 n 时，算法在最坏输入下的效率；
• 最优效率$C_{best}(n)$：输入规模为 n 时，算法在最好输入下的效率；
• 平均效率$C_{avg}(n)$：输入规模为 n 时，算法在随机输入下的效率；

选择排序算法效率分析#

'''
输入: 一个杂乱的数据 A[0...n − 1]
输出: 升序排列的数据 A[0...n − 1]
'''
function Selection_Sort(A[0...n − 1])
    for i = (0 , n − 2) do
        min = i //min 为最小元素索引
        for j = (i + 1 , n − 1) do
            if A[j] < A[min] then
                min = j
            end if
        end for
        swap A[i] and A[min]
    end for
end function

$$ C_{best}(n)=C^2_n $$

$$ C_{worst}(n)=C^2_n $$

$$ C_{avg}(n)=C^2_n $$

$$ \frac{1}{2}n(n-1)\in \theta (n^2) $$

冒泡排序算法效率分析#

'''
输入: 一个杂乱的数据 A[0...n − 1]
输出: 升序排列的数据 A[0...n − 1]
'''
function Bubble_Sort(A[0...n − 1])
    for i = (0 , n − 2) do
        for j = (0 , n − 2 − i) do
            if A[j + 1] < A[j] then
                swap A[j] and A[j + 1]
            end if
        end for
    end for
end function

$$ C_{best}(n)=C^2_n $$

$$ C_{worst}(n)=C^2_n $$

$$ C_{avg}(n)=C^2_n \in \theta(n^2) $$

基本效率类型#

$$ 1<log_n<n<nlog_n<n^2<n^3<2^n<n! $$