05. 树

基本概念

树的定义（在任意非空树中）

必有一个称为根的结点。
当 n>1（结点树）时，其余结点可分为 m（m>0）个互不相交的有限集 T1，T2······T_m。
其中每一个集合本身又是一颗树，称为根的子树。

特点

非空树中至少有一个根结点。
树中各子树是互不相交的集合。
任意结点都可以有零个或多个直接后继结点，但至多只有一个直接前趋结点。
叶结点无后继，根结点无前趋。

关键词

结点：树中的元素，包括数据项及若干指向其子树的分支。
结点的度：结点拥有的子树数。
树的度：一个树中最大的结点的度。
叶子结点：度为 0 的结点，也叫终端结点。
分支结点：度不为 0 的结点，也叫非终端结点。
内部结点：除根结点外的分支结点。
孩子结点：结点子树的根，称为该结点的孩子。
双亲结点：孩子结点的上层结点，称为该结点的双亲。
兄弟结点：同一双亲的孩子之间互称为兄弟。
堂兄弟结点：其双亲在同一层的结点互称为堂兄弟。
树的层次：从根结点算起，根为第一层，它的孩子为第二层······
树的深度：树中结点的最大层次数。
有序树和无序树：如果将树中结点的各子树看成从左至右有次序的(即不能互换)，则称该树为有序树，否则称无序树。有序树最左边的子树的根称为第一个孩子，最右边的称为最后一个孩子。
森林：m(m>=0)颗互不相交的树的集合。
祖先：结点的祖先是从根到该结点所经分支上的所有结点。
子孙：以某结点为根的子树中的任一结点都称为该结点的子孙。

基本操作

初始化、求根、求双亲、求孩子结点、求右兄弟、建树、插入子树操作、删除子树操作、遍历操作、清除操作。

应用场景

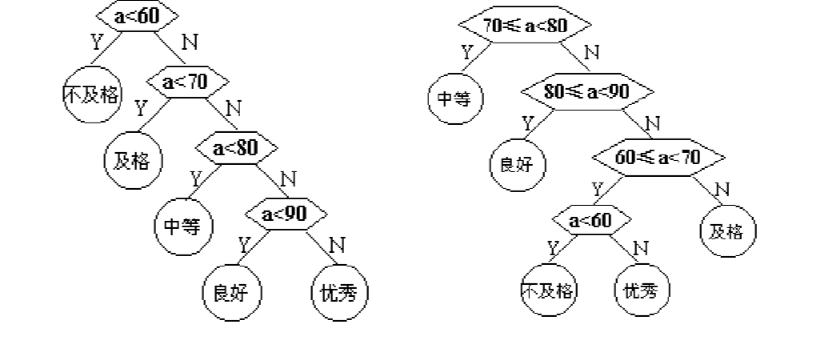
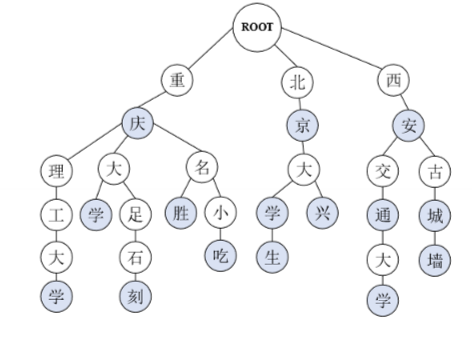
决策树、二叉排序树、句法依存树······

二叉树

基础概念

每个结点至多有两棵子树。
不存在度大于 2 的结点。
子树有左右之分，次序不能任意颠倒。
二叉树不是一种特殊的树，只是一种特殊的树形结构。

满二叉树

深度为 k 的满二叉树，有 2^k - 1 个结点。

2^{0} + \dots \dots + 2^{k - 1} = 2^{k} - 1

2^k - 1，是深度为 k 的二叉树所具有的最大结点个数。
每层上的结点数都达到最大值。
只有度为 0 和度为 2 的结点。
每个结点均有两棵高度相同的子树。
叶子结点都在树的最下一层。

判断一个树是否是完全二叉树：

思路：从上到下，右到左扫描，第一个度小于 2 的之后的每一个结点都必须是叶子结点。

foreach node in one_layer
begin:
	if node 有两个孩子，则 continue;
	if node 无左孩子但有右孩子，则 return False;
	if (node 有一个左孩子)||(node 是叶子),则:
		foreachafnode in NODES(node 之后的结点集)
			if afnode 不是叶子,则 return False;
endforeach
return Ture;

完全二叉树

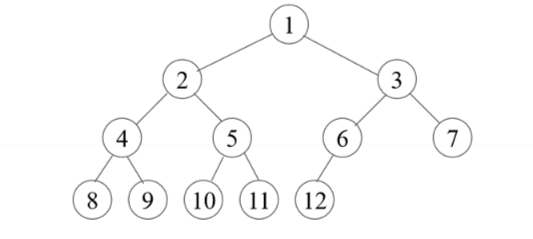
对比满二叉树，次序是一样的，最后一层只缺少右边的若干结点。
叶子结点只可能在最大的两层上出现。
对任意结点，若其右子树的深度为 L，则其左子树的深度必为 L 或 L+1。
除最后一层外，每一层的结点数均达到最大值。

性质

二叉树的第 i 层至多有 2^{i-1}个结点（i>=1）。
深度为 k 的二叉树，至多有 2^k - 1 个结点。
对任意二叉树 T，如果其终端结点数为 n0，度为 2 的结点数为 n2，则 n0 = n2 + 1。
具有 n 个结点的完全二叉树的深度为[log_2 n ] + 1。
对于有 n 个结点的完全二叉树的结点按层序编号（从第一层到最后一层，每层从左到右），则对任一结点（1<= i <=n），有：
- 如果 i=1，则结点 i 是根结点，无双亲，否则，其双亲结点是[i/2]
- 如果 2i>n，则结点 i 无左孩子（结点 i 为叶子），否则其左孩子是节点 2i。
- 如果 2i + 1>n，则结点 i 无右孩子，否则右左孩子是节点 2i。

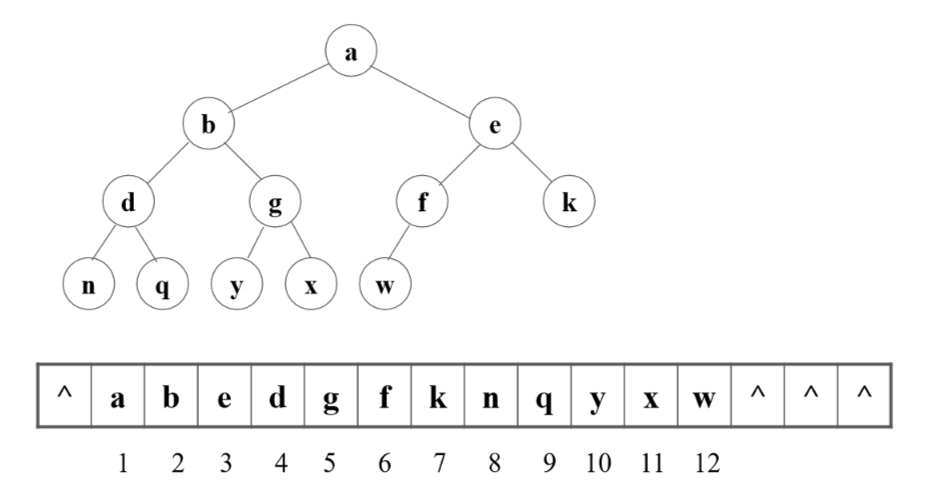
存储

顺序存储

将任意二叉树修补为完全二叉树，用顺序表对元素进行存储，原二叉树空缺的结点，其顺序表相应单元置空：

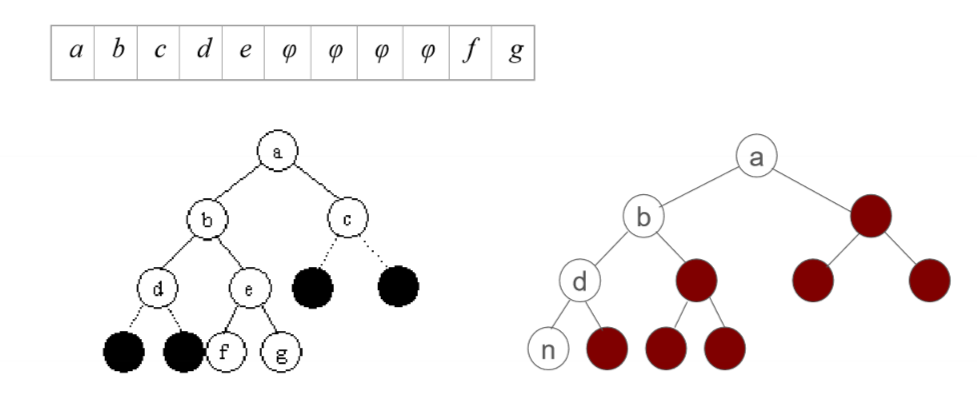
链式存储

结点有三个域：数据域、指向左、右子树的指针域：

cpp

struct btnode{
    char c;
    btnode* lchild;
    btnode* rchild;
    btnode(char c):
        c(c),lchild(NULL),rchild(NULL){

        }
};

基本操作

创建二叉树：

思路：

按先序序列建立二叉链表。
abd···ef··g··（要求会画图）
- 建立根结点
- 先序建立左子树
- 先序建立右子树

cpp

int x = 0;
// char str[] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c', '#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#',};
btnode* creatTree(char *str){
    cout << x << "," << str[x] << "; ";
    if(x >= 23 || str[x] == '#'){
        x += 1;
        return NULL;
    }
    btnode* cur_node = new btnode(str[x]);//建立当前树的根接节点
    x += 1;
    cur_node->lchild = creatTree(str);
    cur_node->rchild = creatTree(str);
 
    return cur_node;
}

计算叶子数：

若树空，return 0；
若树 t 只有唯一的根，则 return 1
否则
- 求该二叉树的左子树的叶子数 m。
- 求该二叉树的右子树的叶子数 n。
- return m+n;

cpp

int countLeaf(btnode *T){
    if(T == NULL){
        return 0;
    }
    if(T->lchild == NULL && T->rchild == NULL){
        return 1;
    }
    int m = countLeaf(T->lchild);
    int n = countLeaf(T->rchild);
    return m+n;
}

计算树的深度：

若树为空，return 0;
否则
- 计算左子树的高度 m
- 计算右子树的高度 n
- return（m>n）？m+1:n+1

cpp

int high(btnode *T){
    if(T == NULL){
        return 0;
    }else{
        int m = high(T->lchild) + 1;
        int n = high(T->rchild) + 1;
        if(m > n){
            return m;
        }else{
            return n;
        }
    }
}

带括号的中缀表达式：

cpp

//仿照中序遍历，只是区分左右子树
void infixExpression(btnode *T){
    if(T != NULL){
        if(T->lchild != NULL)cout << "(";
        
        infixExpression(T->lchild);
        cout << T->c;
        infixExpression(T->rchild);
        
        if(T->rchild != NULL)cout << ")";
    }
}

遍历

先序遍历（根左右）：

cpp

void preorder(btnode *T){
    if(T != NULL){
        cout << T->c << ", ";
        preorder(T->lchild);
        preorder(T->rchild);
    }else{
        cout << "#, ";//输出占位符，保持结构
    }
}

中序遍历（左根右）：

cpp

void inorder(btnode *T){
    if(T != NULL){
        inorder(T->lchild);
        cout << T->c << ", ";
        inorder(T->rchild);
    }else{
        cout << "#, ";//输出占位符，保持结构
    }
}

后序遍历（左右根）：

cpp

void postorder(btnode *T){
    if(T != NULL){
        postorder(T->lchild);
        postorder(T->rchild);
        cout << T->c << ", ";
    }else{
        cout << "#, ";//输出占位符，保持结构
    }
}

主函数：

cpp

int main(){
    cout << "Create Tree" << endl;
    char str[] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c', '#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#',};
    btnode* bt_tree = creatTree(str);
    //遍历
    cout << endl << endl << "preorder,inorder,postorder:" << endl;
    preorder(bt_tree);
    cout << endl;
    inorder(bt_tree);
    cout << endl;
    postorder(bt_tree);
    //计算叶子数
    cout << endl << endl;
    int x = countLeaf(bt_tree);
    cout << "coutLeaf:" << x << endl;
    //计算树深
    cout << endl << "high=" << high(bt_tree) << endl;
    //中缀表达式
    cout << endl << "infixExpression:" << endl;
    infixExpression(bt_tree);
    return 0;
}

输出：

cpp

Create Tree
0,-; 1,+; 2,a; 3,#; 4,#; 5,*; 6,b; 7,#; 8,#; 9,-; 10,c; 11,#; 12,#; 13,d; 14,#; 15,#; 16,/; 17,e; 18,#; 19,#; 20,f; 21,#; 22,#; 

preorder,inorder,postorder:
-, +, a, #, #, *, b, #, #, -, c, #, #, d, #, #, /, e, #, #, f, #, #,
#, a, #, +, #, b, #, *, #, c, #, -, #, d, #, -, #, e, #, /, #, f, #,
#, #, a, #, #, b, #, #, c, #, #, d, -, *, +, #, #, e, #, #, f, /, -, 

coutLeaf:6

high=5

infixExpression:
((a+(b*(c-d)))-(e/f))

层序遍历：

思路：利用队列

cpp

//层序遍历二叉树
void printBinTree(btnode* root) {
    queue<btnode*> q;
    btnode* b;

    //树为空
    if (root == NULL) {
        cout << "treeNode is empty!" <<endl;
        return;
    }

    //根节点入队
    q.push(root);

    while (!q.empty()) {

        b = q.front();  //拿到队头，队头出队
        q.pop();
        cout << b->c << ", ";  //打印对头的数据

        //对头的左孩子存在就入队
        if (b->lchild) {
            q.push(b->lchild);
        }

        //对头的右孩子存在就入队
        if (b->rchild) {
            q.push(b->rchild);   
        }
    }
}


int main(){
    cout << "Create Tree" << endl;
    char str[] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c', '#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#',};
    btnode* bt_tree = creatTree(str);   
    cout << endl;
    printBinTree(bt_tree);
    return 0;
}

递归算法的非递归描述

cpp

//中序遍历为例
void nonRecInorder(btnode *T){
    btnode * p = T;
    vector<btnode*> st;
    if(T != NULL){
        st.push_back(p);
    }else{
        return;
    }
    p = p->lchild;
    while(1){
        while(p != NULL){//右
            st.push_back(p);//同时压栈
            p = p->lchild;
        }
        if(!st.empty()){
            p = st.back();
            st.pop_back();
            cout << p->c << ", ";//中
            p = p->rchild;//左
        }else{
            return;
        }
    }
}

int main(){
    cout << "Create Tree" << endl;
    char str[] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c', '#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#',};
    btnode* bt_tree = creatTree(str);
    cout << endl;
    nonRecInorder(bt_tree);
    return 0;
}

cpp

//计算叶子数的非递归描述
int nonRecCountLeaf(btnode *T){  
  if(T == NULL)
    return 0;
  int num = 0;
  vector <btnode*> st;
  while (T != NULL || !st.empty())
  {
    while (T != NULL)
    {
      cout << "node:" << T->c << endl;//print
      st.push_back(T);
      T = T->lchild;
    }
    if (!st.empty())
    {
      T = st.back();//从空那边回来
      st.pop_back();
      if(T->lchild == NULL && T->rchild == NULL)//判断是否为叶子节点
        num++;
      T = T -> rchild;
    }
  }
  return num;
}


int main(){
    cout << "Create Tree" << endl;
    char str[] = {'-', '+', 'a', '#', '#', '*', 'b', '#', '#', '-', 'c', '#', '#', 'd', '#', '#', '/', 'e', '#', '#', 'f', '#', '#',};
    btnode* bt_tree = creatTree(str);   
    cout << endl;
    int x = nonRecCountLeaf(bt_tree);
    cout << endl << "num:" << x;

    return 0;
}

树

树的表示

双亲表示法：

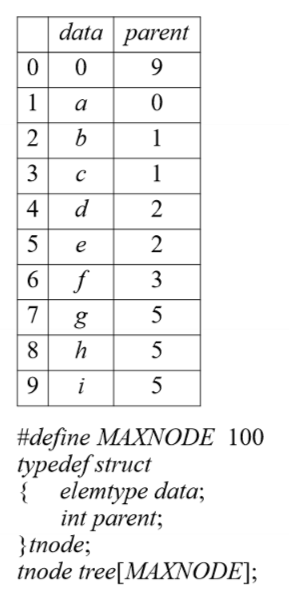
孩子链法：

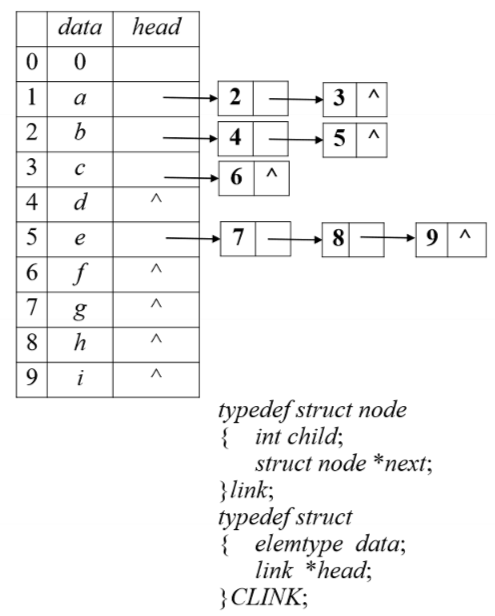
转换

孩子兄弟表示法：

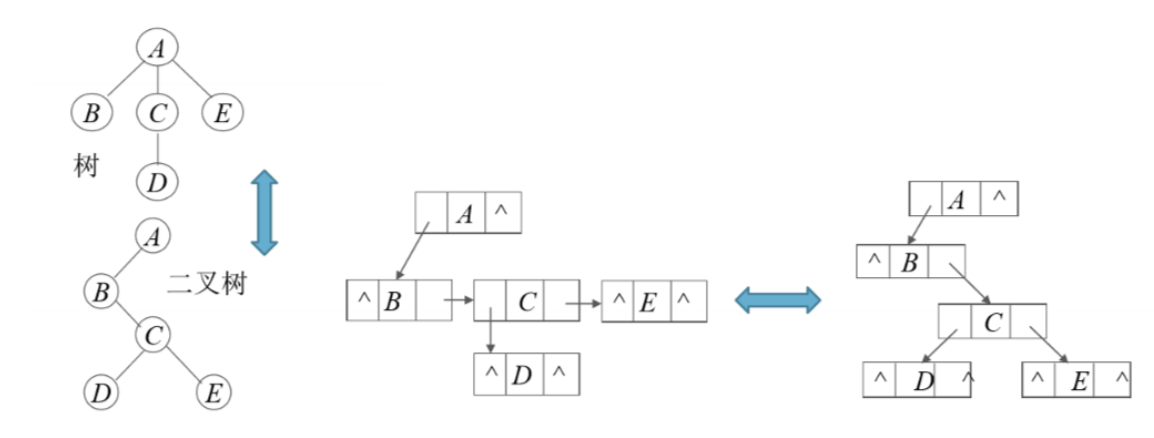
将树转换为二叉树：

加线：在兄弟之间加一连线。
抹线：对每个结点，除其第一孩子外，去除其与其余孩子之间的关系。
旋转：以树的根结点为轴心，将整棵树顺时针转 45`。
树转换为二叉树其右子树一定为空。

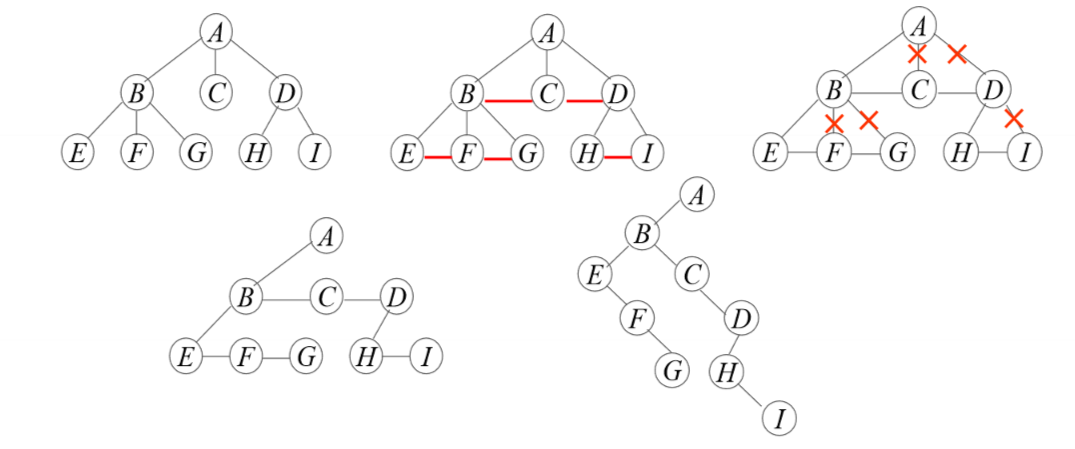
二叉树转换为树：

加线：若 p 结点是双亲结点的左孩子则将 p 的右孩子，右孩子的右孩子，······沿分支找到的所有右孩子，都与 p 的双亲连起来。
抹线：抹掉原二叉树中双亲与右孩子之间的连线。
调整：将结点按层次排列，形成树结构。

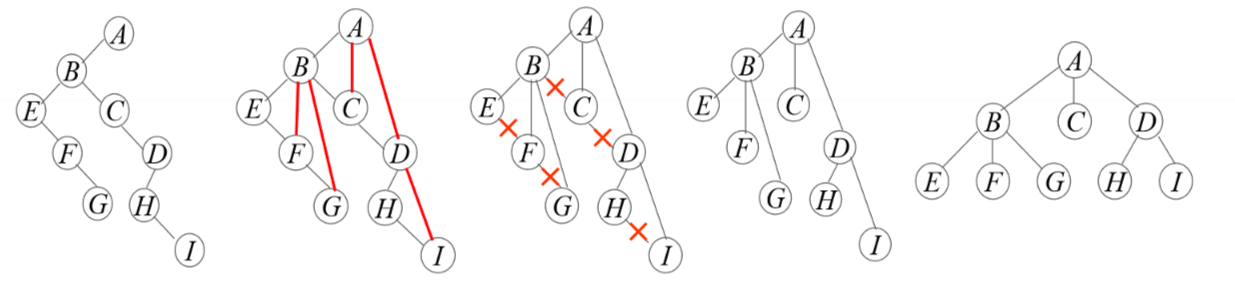
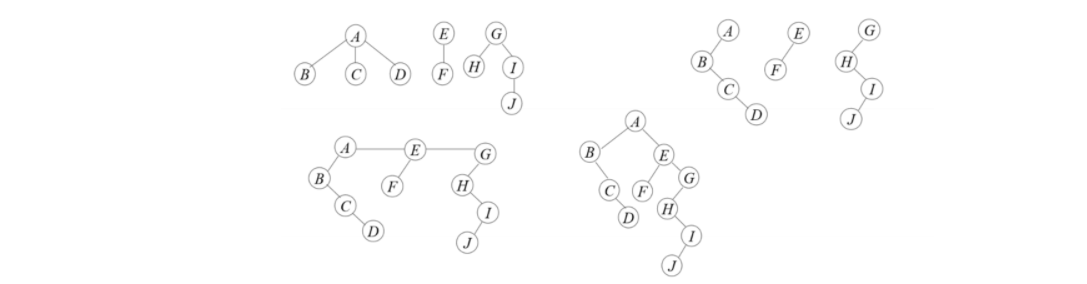
森林转换为二叉树：将各棵树分别转换成二叉树，将每棵树的根结点用线相连。

哈夫曼树

基础概念

路径：若树中存在某个结点序列 k_1,k_2······k_j。满足 k_i 是 k_{i+1}的双亲，则该结点序列是树上的一条路径。
树的路径长度是指树根到树中每一个结点的路径之和。
完全二叉树的路径长度最短。
结点的权：给树的结点赋以一定意义的数值，称为结点的全权。
结点的带权路径长度：从树根到某个结点的路径长度与该结点的权的积。
树的带权路径长度：树中所有叶子结点的带权路径长度之和。
哈夫曼树的定义：
- 由 n 个带权叶子结点构成的二叉树具有不同形态。
- 其中 WPL 最小的二叉树
- 又叫做最优二叉树，或最佳判定树。
$w p l = \sum_{k = 1}^{n} w_{k} l_{k}$
其中，w_k 是第 i 个叶子结点的权值，l_k 是根到第 i 个叶子结点的路径长度。

创建哈夫曼树与哈夫曼编码

创建：

初始化 n 个权值，到 forest 的前 n 个单元，作为 forest 中 n 个孤立的根结点。

将前 n 个单元的双亲、左、右孩子指针均置为 0。
不妨将下标为 0 的单元留空。

foreach pos in(n+1~2n-1)
begin
	进行 1 次合并，从 froest 中删除两棵树，生成 1 棵新树：
		从 forest 的根结点中，选取根结点权值最小、次小的两棵树 p1 和 p2。
		合并 forest[p1]和 forest[p2]，生成新根结点 forest[pos]
			置 forest[pos].w = forest[p1].w + forest[p2].w
			置 forest[p1]和 forest[p2]分别为 forest[pos]的左右孩子。
			置 forest[p1]和 forest[p2]的双亲为 forest[pos]
endforeach
return

**前缀码：**任一字符的编码，不能是其他字符的前缀。

将值作为结点的值，将权重作为边。
构造最优二叉树
将树中每个结点的左分支置为 0，右分支置为 1。
从根到叶子结点的一个标号序列，就是该叶子结点的编码。

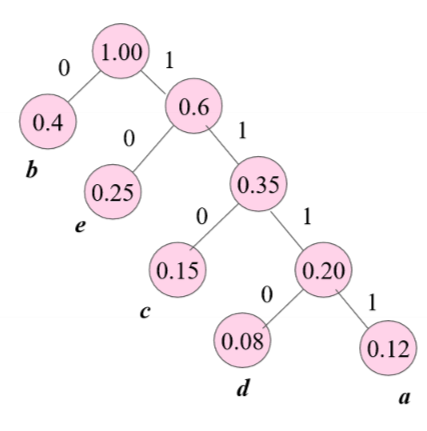
原因：没有一片树叶是其他树叶的祖先，所以叶子结点编码不可能是其他叶子结点编码的前缀。

数据处理

python

data = []
with open("huffmandata.txt", "r", encoding="utf-8") as f:
    data = f.read()
data[1]

'b'

python

nums = [0,0,0,0,0]
for i in data:
    if(i == 'a'):
        nums[0] += 1
    if(i == 'b'):
        nums[1] += 1
    if(i == 'c'):
        nums[2] += 1
    if(i == 'd'):
        nums[3] += 1
    if(i == 'e'):
        nums[4] += 1
nums

[398964, 400200, 399318, 400002, 401516]

python

weight = [0, 0, 0, 0, 0]
for i in range(5):
    weight[i] = nums[i]/len(data)
weight

[0.199482, 0.2001, 0.199659, 0.200001, 0.200758]

python

op = [0, 0.199482, 0.2001, 0.199659, 0.200001, 0.200758, 0, 0, 0, 0, ]
mem = [1,1,1,1,1,1,1,1,1,1,]
len(mem)

生成哈夫曼树

python

op = [0.199482, 0.2001, 0.199659, 0.200001, 0.200758, 0, 0, 0, 0,]
mem = [1,1,1,1,1,1,1,1,1,]  # 标记是否用过
temp = []  # 存储逆序前的哈夫曼树
weizhi = []

n = len(weight)
c = n
for i in range(n, 2*n-1):
    min_1 = 1
    min_1_index = 0
    min_2 = 1
    min_2_index = 0

    for j in range(0, c):
        if(op[j]*mem[j] < min_1):
            min_1 = op[j]
            min_1_index = j
    for j in range(0, c):
        if((op[j]*mem[j] < min_2) & (op[j] != min_1)):
            min_2 = op[j]
            min_2_index = j
    
    # 标记
    mem[min_1_index] = 20  # 这里只要是一个较大的数就行
    mem[min_2_index] = 20
    temp.append(op[min_1_index])
    temp.append(op[min_2_index])
    print(min_1_index,min_2_index)
    if(min_1_index < n):
        weizhi.append(min_1_index)
    if(min_2_index < n):
        weizhi.append(min_2_index)
    op[i] = op[min_1_index] + op[min_2_index]
    c += 1

# print(op)
temp.append(1)
# 逆序
huffmantree = [0,]
for i in range(len(op)-1,-1,-1):
    huffmantree.append(temp[i])

print(weizhi)
huffmantree

0 2
3 1
4 5
6 7
[0, 2, 3, 1, 4]



[0,
 1,
 0.599899,
 0.40010100000000004,
 0.39914099999999997,
 0.200758,
 0.2001,
 0.200001,
 0.199659,
 0.199482]

生成最优前缀码

python

l = len(huffmantree)

python

# 生成的列表方便逆序生成正确的编码
codes = []
for i in range(l-1, int(l/2)-1, -1):
    # print(i)
    codes.append(-1)
    while(int(i/2) != 0):
        if(i%2 == 1):
            codes.append(1)
        else:
            codes.append(0)
        i = int(i/2)
codes

[-1, 1, 0, 0, -1, 0, 0, 0, -1, 1, 1, -1, 0, 1, -1, 1, 0]

python

# 找到对应的位置
element_src = ['a', 'b', 'c', 'd', 'e']
element = ['x','x','x','x','x']
for i in range(0, len(element_src)):
    element[i] = element_src[weizhi[i]]

element

['a', 'c', 'd', 'b', 'e']

python

ele_encode = {}
s = ""
j = 0
for i in range(len(codes)-1,-1,-1):
    if(codes[i] == -1):
        ele_encode[element[j]] = s
        j += 1
        s = ""
    else:
        s += str(codes[i])

ele_encode

{'a': '01', 'c': '10', 'd': '11', 'b': '000', 'e': '001'}

05. 树 ​

基本概念 ​

树的定义（在任意非空树中） ​

特点 ​

关键词 ​

基本操作 ​

应用场景 ​

二叉树 ​

基础概念 ​

满二叉树 ​

完全二叉树 ​

性质 ​

存储 ​

顺序存储 ​

链式存储 ​

基本操作 ​

创建二叉树： ​

计算叶子数： ​

计算树的深度： ​

带括号的中缀表达式： ​

遍历 ​

先序遍历（根左右）： ​

中序遍历（左根右）： ​

后序遍历（左右根）： ​

主函数： ​

输出： ​

层序遍历： ​

递归算法的非递归描述 ​

树 ​

树的表示 ​

转换 ​

哈夫曼树 ​

基础概念 ​

创建哈夫曼树与哈夫曼编码 ​

数据处理 ​

生成哈夫曼树 ​

生成最优前缀码 ​

05. 树

基本概念

树的定义（在任意非空树中）

特点

关键词

基本操作

应用场景

二叉树

基础概念

满二叉树

完全二叉树

性质

存储

顺序存储

链式存储

基本操作

创建二叉树：

计算叶子数：

计算树的深度：

带括号的中缀表达式：

遍历

先序遍历（根左右）：

中序遍历（左根右）：

后序遍历（左右根）：

主函数：

输出：

层序遍历：

递归算法的非递归描述

树

树的表示

转换

哈夫曼树

基础概念

创建哈夫曼树与哈夫曼编码

数据处理

生成哈夫曼树

生成最优前缀码