智库

11. 动态规划 ​

概述 ​

如果原问题是由交叠的子问题构成（递归调用），动态规划对每个子问题只求解一次，并把结果记录在表中，递推计算得到原始问题的解。

它是只求一次子问题，所以相比于递归暴力求解就复杂度降低了

但相对于记忆化搜索，时间复杂度是一样的，只是记忆化搜索需要用到递归，是一种“从顶到底”的方法，而动态规划是一种“从底到顶”的方法。

动态规划为什么叫做动态规划，就是因为当前你需要做决策，而当前的决策会需要选择不同的以前的最优决策，这个规划是动态的。

解题步骤

  • 可分为多个相关子问题，子问题的解可以被重复使用(下方例子中是 F 数组与 value 数组来保留子问题解的)，这也是相比于递归暴力求解效率提高的关键，下方前两个例子会简单比较效率，第二个例子由于数据不具代表性，所以有所差异

  • 动态规划的关键就是如何根据条件从上一个子问题的最优解到该现状的途径(写出递推关系)

  • 然后该途径会有很多种再根据问题通过 min 或 max 求得哎现状的最优解，该现状当然也又有可能出现在之后现状的子问题当中

  • 写出初始条件

  • (之前自己理解的误区)在理解中不要仅仅注意到递推关系，比如背包问题中之前理解错了是总是感觉包括第 i 件物品的组合肯定肯定比不包括第 i 件物品的组合的总价值大，这种理解的错法在于没有真正理解到动态规划的自下而上，而仅仅看到了递推关系，实际上这里 F(i ,j)，变的不仅仅是 i，还有 j，相当于你不包括第 i 件物品，那么你就有更多的空间去选择其他的，总之就是包含第 i 件与不包含第 i 件的前一子组合的子组合是不同的。

求斐波拉契数列：

image-20211105143110619

币值最大化 ​

给定一排硬币，这些整数不一定两两相同，使得在其原始位置互不相邻的条件下，所选的硬币金额最大

  • 包括最后一枚的：c_n + F(n-2)

  • 不包括最后一枚的：F(n-1)

python
# 动态规划实现
def CoinRow1(coins):
	F = [0]
	F.append(coins[0])
	for i in range(1, len(coins)):
		F.append(max(coins[i] + F[i-1], F[i])) 

	return F[len(coins)]

test_coin = [5, 1, 2, 10, 6, 2]
CoinRow1(test_coin)
python
# 递归实现
def CoinRow2(coins, i):
	if i == 0:
		return 0
	if i == 1:
		return coins[0]
	return max((coins[i] + CoinRow2(coins, i - 2)), CoinRow2(coins, i - 1))

test_coin = [5, 1, 2, 10, 6, 2]
CoinRow2(test_coin, len(test_coin)-1)

找零 ​

m 种币值，找零金额为 n，求最少使用多少枚币

获取 n 的途径只能是：在总金额为n−dj的一堆硬币加入一个面值为dj的硬币，其中j=1,2,...,m,并且n≥dj。因此我们只需考虑所有满足上述要求的dj并选择使得F(n−dj)+1最小的dj即可。由于 1 是常量，我们显然可以先找出最小的F(n−dj)，然后加 1 即可，公式：

{F(n)=minj:n≥dj{F(n−dj)}+1n>0F(0)=0
python
# 动态规划实现
def ChangeMaking1(D, n):
	F = [0]
	for i in range(1, n+1):
		temp = float('inf')
		j = 0
		while(j < len(D) and i >= D[j]):
			temp = min(F[i-D[j]], temp)
			j += 1
		F.append(temp + 1)

	return F[n]

ChangeMaking1([1,3,4], 6)
python
# 递归实现
def ChangeMaking2(D, n):
	min_count = n
	if n in D:
		return 1
	for value in [i for i in D if i <= n]:
		count = 1 + ChangeMaking2(D, n - value)
		if count < min_count:
			min_count = count	
	
	return min_count

ChangeMaking2([1,3,4], 6)

背包问题 ​

image-20211105151844839
  • 记忆化搜索是一种“从顶到底”的方法
  • 动态规划是一种“从底到顶”的方法

两者的时间复杂度是一样的，只是记忆化搜索需要用到递归。

基本背包问题解法 ​

python
def bag(n, c, w, v):
    # 置零，表示初始状态
    value = [[0 for j in range(c + 1)] for i in range(n + 1)]
    for i in range(1, n + 1):
        for j in range(1, c + 1):
            value[i][j] = value[i - 1][j]
            # 背包总容量够放当前物体，遍历前一个状态考虑是否置换，相当于递推关系中的 max 操作
            if j >= w[i - 1] and value[i][j] < value[i - 1][j - w[i - 1]] + v[i - 1]:
                value[i][j] = value[i - 1][j - w[i - 1]] + v[i - 1]
    return value
# test
n = 4  # 物品的数量，
c = 5 # 书包能承受的重量，
w = [2, 1, 3, 2] # 每个物品的重量，
v = [12, 10, 20, 15] # 每个物品的价值

value = bag(n, c, w, v)
for i in value:
    print(i)
print(value[-1][-1])
python
# output
[0, 0, 0, 0, 0, 0]
[0, 0, 12, 12, 12, 12]
[0, 10, 12, 22, 22, 22]
[0, 10, 12, 22, 30, 32]
[0, 10, 15, 25, 30, 37]
37

注意，这里代码容易迷惑的地方就是：

  • value[i - 1][j]代表的就是前一项，dp表默认填充了0；
  • 而w[i - 1]和v[i - 1]代表的是当前项，这里的i是从 1 开始的，所以要减去 1。

回溯找组合 ​

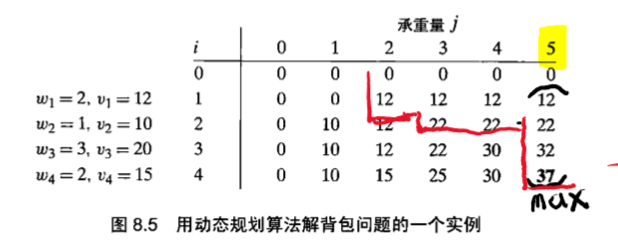
image-20211105152058485
python
def show(n, c, w, value):
    print('最大价值为:', value[n][c])
    x = [False for i in range(n)]
    j = c
    # 回溯
    for i in range(n, 0, -1):
        if value[i][j] > value[i - 1][j]:
            x[i - 1] = True
            j -= w[i - 1]
    print('背包中所装物品为:')
    for i in range(n):
        if x[i]:
            print('第', i+1, '个', end=',')

show(n, c, w, value)
python
# output
最大价值为: 37
背包中所装物品为:
第 1 个,第 2 个,第 4 个,

带记忆功能的背包问题解法 ​

python
import numpy as np
# 生成第一列，第一行为 0，其余为 null(-1 表示)的二维数组
value = np.zeros([n+1,c+1])
value[:], value[0,:], value[:,0] = -1, 0, 0  # 利用了 numpy 的广播机制
value = list(value)
# 自上而下了，从 i=4,j=5 开始找自己需要的子问题解
def bag_imporve_time(i, j, w, v):
    if value[i][j] < 0:
        if j < w[i-1]:
            temp = bag_imporve_time(i-1, j, w, v)
        else:
            temp = max(bag_imporve_time(i-1, j, w, v), bag_imporve_time(i-1, j-w[i-1], w, v) + v[i-1])
        value[i][j] = temp

    return value[i][j]

# test
n = 4  # 物品的数量，
c = 5 # 书包能承受的重量，
w = [2, 1, 3, 2] # 每个物品的重量，
v = [12, 10, 20, 15] # 每个物品的价值
bag_imporve_time(n, c, w, v)
python
37
python
# -1 代表了减少的计算
value
python
[array([0., 0., 0., 0., 0., 0.]),
 array([ 0.,  0., 12., 12., 12., 12.]),
 array([ 0., -1., 12., 22., -1., 22.]),
 array([ 0., -1., -1., 22., -1., 32.]),
 array([ 0., -1., -1., -1., -1., 37.])]

优化空间的尾部迭代法 ​

python
def bag_imporve_space(n, c, w, v):
    # 仅记录最优解
    values = [0 for i in range(c+1)]
    for i in range(1, n + 1):
        for j in range(c, 0, -1):
            # 背包总容量够放当前物体，遍历前一个状态考虑是否置换
            if j >= w[i-1]:
                values[j] = max(values[j-w[i-1]]+v[i-1], values[j])
    
    return values

n = 4  # 物品的数量，
c = 5 # 书包能承受的重量，
w = [2, 1, 3, 2] # 每个物品的重量，
v = [12, 10, 20, 15] # 每个物品的价值
bag_imporve_space(n, c, w, v)
python
[0, 10, 15, 25, 30, 37]

动态规划进阶 ​

最优二叉查找树 ​

TODO

图传递闭包问题 ​

TODO

完全最短路径问题 ​

TODO

矩阵链乘计算 ​

TODO

最长递增子序列 ​

TODO

编辑距离问题 ​

TODO